Skip to main content

1. Graphs Concept

A Graph is a non-linear data structure consisting of nodes and edges. The nodes are formally called vertices, and the edges are lines or arcs that connect any two nodes in the graph.

Graphs are used to solve many real-world problems. They are used to represent networks, such as social networks, transportation networks (roads and cities), or computer networks.

1.1 Graph Terminology

  • Vertex (or Node): The fundamental unit of the graph.
  • Edge: A line that connects two vertices.
  • Path: A sequence of vertices connected by edges.
  • Cycle: A path that starts and ends at the same vertex. A graph with no cycles is acyclic.
  • Connected Graph: An undirected graph where there is a path between any two vertices.
  • Weighted Graph: Each edge is assigned a numerical value or "weight," often representing cost or distance.
  • Unweighted Graph: Edges do not have weights.

1.2 Graph Analogy

Imagine a social network like Facebook or LinkedIn.

  • Each person is a Vertex (Node).
  • The friendship or connection between two people is an Edge.
  • If the friendship is mutual (i.e. Facebook), it's an undirected graph.
  • If you can "follow" someone without them following you back (i.e. Twitter), it's a directed graph.

1.3 Types of Graph

1.3.1 Undirected Graph

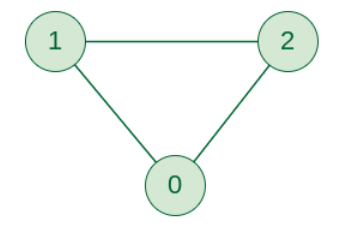
In an Undirected Graph, edges represent a mutual, bidirectional relationship. An edge (u, v) is identical to an edge (v, u). There is no "direction" to the connection.

  • Analogy: A friendship on Facebook or a two-way street. If A is friends with B, then B is automatically friends with A.
  • Degree: The "degree" of a vertex is simply the total number of edges connected to it.

1.3.2 Directed Graph

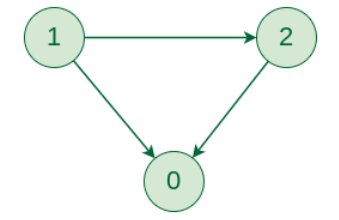
In a Directed Graph (or Digraph), edges are one-way streets. An edge (u, v) represents a connection from u to v, but it does not imply a connection from v to u.

  • Analogy: Following someone on Twitter or a one-way street. A can follow B (an edge A -> B), but B does not have to follow A back. An edge B -> A would be a separate, distinct edge.
  • Degree: Degree is split into two types:
    • In-degree: The number of edges pointing to the vertex.
    • Out-degree: The number of edges pointing away from the vertex.
Back to top