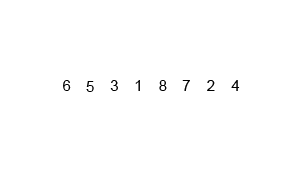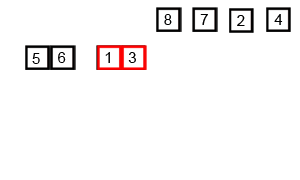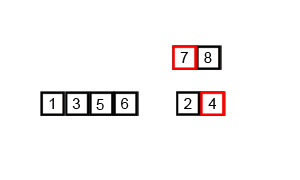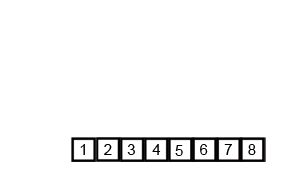Skip to main content

1. Understanding Merge Sort

What is Merge Sort?

Merge Sort is an efficient, comparison-based sorting algorithm that uses a "divide and conquer" strategy. In simple terms, it repeatedly breaks down a list into several sub-lists until each sub-list contains only one item (which is considered sorted). Then, it merges those sub-lists back together in a sorted manner.

How Does it Work?

The process can be broken down into two main phases:

  1. Divide Phase: The main, unsorted list is recursively divided in half. This continues until all the resulting sub-lists have only one element.
  2. Conquer (Merge) Phase: Starting with the single-element lists, the algorithm repeatedly merges pairs of adjacent sub-lists. During each merge, it compares the elements from the two lists and combines them into a new, larger, sorted list. This continues until all the sub-lists have been merged back into a single, completely sorted list.

Visualization Explanation from the GIF

The GIF you provided is a perfect illustration of this "divide and conquer" method. Let's break it down step-by-step.

Merge-sort-example-300px.gif

  1. The Start: The animation begins with an unsorted list of numbers: [6, 5, 3, 1, 8, 7, 2, 4].

  2. The "Divide" Phase:

    • First Split: The entire list is split into two halves: [6, 5, 3, 1] and [8, 7, 2, 4].
    • Second Split: Each of those halves is split again: [6, 5], [3, 1] and [8, 7], [2, 4].
    • Final Split: The splitting continues until we have eight separate lists, each containing just one number: [6], [5], [3], [1], [8], [7], [2], [4]. At this point, the "divide" phase is complete. A list with one item is inherently sorted.

  3. The "Conquer (Merge)" Phase: Now, the algorithm starts merging these small lists back together in sorted order.

    • First Merge: It merges adjacent pairs. [5] and [6] are compared and merged to form [5, 6]. [1] and [3] are merged to form [1, 3]. Similarly, [7, 8] and [2, 4] are created. We now have four sorted sub-lists: [5, 6], [1, 3], [7, 8], and [2, 4].
    • Second Merge: The process repeats with these new, larger sorted lists. [5, 6] and [1, 3] are merged. The algorithm compares the first element of each list (1 vs 5), takes the 1, then compares 3 and 5, takes the 3
Back to top