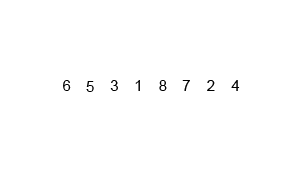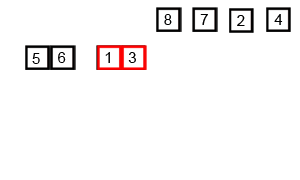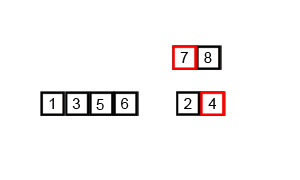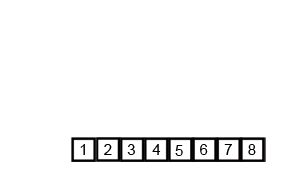1. Understanding Merge Sort
What is Merge Sort?
Merge Sort is an efficient, comparison-based sorting algorithm that uses a "divide and conquer" strategy. In simple terms, it repeatedly breaks down a list into several sub-lists until each sub-list contains only one item (which is considered sorted). Then, it merges those sub-lists back together in a sorted manner.
How Does it Work?
The process can be broken down into two main phases:
- Divide Phase: The main, unsorted list is recursively divided in half. This continues until all the resulting sub-lists have only one element.
- Conquer (Merge) Phase: Starting with the single-element lists, the algorithm repeatedly merges pairs of adjacent sub-lists. During each merge, it compares the elements from the two lists and combines them into a new, larger, sorted list. This continues until all the sub-lists have been merged back into a single, completely sorted list.
Visualization Explanation
-
The Start: The animation begins with an unsorted list of numbers:
[6, 5, 3, 1, 8, 7, 2, 4]. -
The "Divide" Phase:
- First Split: The entire list is split into two halves:
[6, 5, 3, 1]and[8, 7, 2, 4]. - Second Split: Each of those halves is split again:
[6, 5],[3, 1]and[8, 7],[2, 4]. - Final Split: The splitting continues until we have eight separate lists, each containing just one number:
[6],[5],[3],[1],[8],[7],[2],[4]. At this point, the "divide" phase is complete. A list with one item is inherently sorted.
- First Split: The entire list is split into two halves:
-
The "Conquer (Merge)" Phase: Now, the algorithm starts merging these small lists back together in sorted order.
- First Merge: It merges adjacent pairs.
[5]and[6]are compared and merged to form[5, 6].[1]and[3]are merged to form[1, 3]. Similarly,[7, 8]and[2, 4]are created. We now have four sorted sub-lists:[5, 6],[1, 3],[7, 8], and[2, 4]. - Second Merge: The process repeats with these new, larger sorted lists.
[5, 6]and[1, 3]are merged. The algorithm compares the first element of each list (1vs5), takes the1, then compares3and5, takes the3
- First Merge: It merges adjacent pairs.
Benefits of Merge Sort
- Predictable Time Complexity: Its greatest strength is its consistent $O(n \log n)$ time complexity, regardless of the initial order of elements (worst, average, and best cases are the same). This makes it very reliable for large datasets.
- Stable Sort: Merge Sort is stable, meaning that if two elements have equal values, their relative order in the original array will be preserved in the sorted array.
- Excellent for External Sorting: It's highly effective for sorting data that is too large to fit into memory (e.g., files on a hard drive) because it reads and processes data in sequential chunks.
- Parallelizable: The "divide" step is easy to parallelize, meaning different parts of the array can be sorted simultaneously on different processor cores, speeding up the process significantly.
Drawbacks of Merge Sort
- Space Complexity: Its main disadvantage is that it requires extra space. It needs an auxiliary array of the same size as the input array, giving it a space complexity of
$O(n)$. This can be a limiting factor in memory-constrained environments like embedded systems. - Slower for Small Datasets: For small lists, the overhead of recursion makes it slower than simpler algorithms like Insertion Sort. This is why many optimized sorting libraries use a hybrid approach.
- Recursive Overhead: The recursive function calls add some overhead to the execution stack, which, while usually minor, can be a consideration.
What is Merge Sort Used For?
Merge Sort's stability and efficiency with large datasets make it very useful in practice.
- Sorting Linked Lists: It is one of the most efficient ways to sort linked lists. Unlike arrays, linked lists are not easily accessible by index, but merging them is a very efficient operation.
- External Sorting: As mentioned, it's a go-to algorithm for sorting massive files that don't fit in RAM.
- Inversion Count Problem: The algorithm can be modified to solve other problems, such as counting the number of inversions in an array efficiently.
- Standard Library Implementations: It forms the basis of many highly optimized, built-in sorting functions in various programming languages, often as part of a hybrid algorithm like Timsort (used in Python and Java), which combines Merge Sort with Insertion Sort.