How to Simplify a Function Using a K-Map
We will focus on the Sum-of-Products (SOP) method, which involves looking for 1s in the map.
Step 1: Create and Fill the Map
Draw the correct K-Map for your number of variables. Look at your function's truth table or list of minterms. Place a 1 in every cell that corresponds to an output of 1. If there are "don't care" conditions, place an X in those cells. Leave all other cells blank (or you can think of them as 0s).
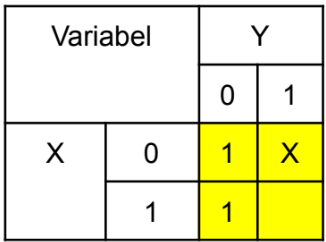
Step 2: Group the 1s
This is the most important step. You need to draw loops around groups of adjacent 1s. Follow these rules:
- Group Size: Groups must contain a power-of-two number of cells (1, 2, 4, 8, or 16). You cannot have a group of 3, 5, or 6 cells.
- Adjacency: You can only group cells that are adjacent, either horizontally or vertically. Remember the "wrap-around" rule for the edges.
- Make Groups as Large as Possible: Always try to make the biggest groups you can. A single group of four is better than two separate groups of two.
- Cover All 1s: Every 1 on the map must be included in at least one group. A 1 can be part of multiple groups if it helps to make other groups larger.
- Use Fewest Groups: Your final goal is to cover all the 1s using the smallest number of groups possible.
- Using "Don't Cares" (X): You can include an X in a group if it helps you make a larger group of 1s. If an X doesn't help create a bigger group, just ignore it and treat it as a 0.
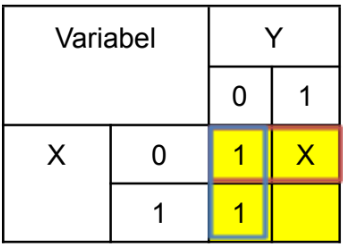
Step 3: Write the Simplified Function
Each group you created will become one term in your final simplified function. To find the term for each group:
- Look at the variables along the rows and columns for that group.
- Find the variable(s) that do not change their value inside the group.
- If a variable stays as
1for the entire group, include it as is (e.g.,A). - If a variable stays as
0for the entire group, include it with a NOT (e.g.,A'). - If a variable changes its value (it is both
0and1) within the group, it is eliminated from that term.
The final simplified function is the OR (sum) of all the terms you derived from each group.

No comments to display
No comments to display