Theory
Boolean algebra is a mathematical system that describes the notations and operations on Boolean values. Boolean values are things that take on one out of two possible values. For example, a bit that can be a 1 or a 0.
Boolean algebra can be used to describe digital systems because digital signals are Boolean values: HIGH/VCC = 1 and LOW/GND = 0. So, a function of a digital system can be analyzed by using boolean algebra.
The laws of Boolean algebra are:
Those laws are used to simplify Boolean algebra expressions. The result is that the amount of components needed to implement a function into a digital system shrinks and so the cost for that system decreases. For example:
(A̅ + B) ∗ (A + B)
= B ∗ (A̅+ A) Inverse of Distributive Law for AND over OR
= B ∗ (1) Idempotent Law for OR
= B Identity Law for AND
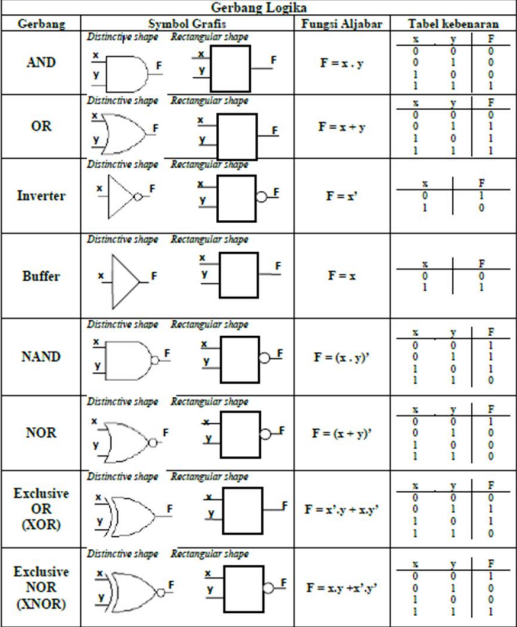
Logic gates are the basic components that make up a digital system. A logic gate implements a logic operation. Below is a list of logic gates with its symbol, function, and truth table: